Loli là một cô bé 5 tuổi và đang được học bảng chữ cái. Điều kiện tiên quyết để Loli viết được một xâu ký tự bất kỳ là Loli phải học hết ký tự trong xâu ký tự đó đã.

Cô giáo giao cho Loli một xâu ~S~ và muốn Loli viết lại xâu đó. Vì Loli lười không muốn học hết bảng chữ cái nên Loli thắc mắc rằng mình cần học ít nhất bao nhiêu chữ cái liên tiếp trong bảng chữ cái tiếng Anh để viết lại xâu ~S~ đó.

Input:

Lấy từ tệp ALPHABET.INP gồm:

• Một dòng duy nhất ghi xâu ~S~ chứa các chữ cái tiếng Anh in thường (độ dài xâu không quá ~10^4~).

Output:

Ghi ra tệp ALPHABET.OUT gồm:

• Một số nguyên là số chữ cái liên tiếp ít nhất Loli cần học.

Ví dụ 1:

ALPHABET.INP

zzzzz

ALPHABET.OUT

1

Ví dụ 2:

ALPHABET.INP

bcf

ALPHABET.OUT

5

Giải thích

• Ở test đầu, Loli chỉ cần học ~1~ ký tự 'z' để viết lại xâu.
• Ở test thứ 2, Loli cần học ~5~ ký tự liên tiếp 'b', 'c', 'd', 'e', 'f' để viết lại xâu.

Loli mới được học về phép tính lũy thừa. Trong buổi học đó, thầy giáo giao cho Loli một bài khá khoai:

Cho một số nguyên dương ~k~, hãy tìm số nguyên dương ~x~ lớn nhất sao cho ~x~ thỏa mãn hai điều kiện:

• ~1\le x < k~;
• ~x! + (x-1)!~ là bội của ~k~, nói cách khác ~x! + (x-1)!~ chia hết cho ~k~.

Input:

Lấy từ tệp WTFACT.INP gồm:

• Một dòng duy nhất ghi số nguyên dương ~k~ ~(2\le k \le 10^9)~.

Output:

Ghi ra tệp WTFACT.OUT gồm:

• Một số nguyên dương là số ~x~ cần tìm. Nếu không có ~x~ thỏa mãn, in ra ~-1~.

Sample Input 1

8

Sample Output 1

7

Giải thích

• Ở test đầu, ~7! + 6! = 5040 + 720 = 5760~, và ~5760~ chia hết cho ~8~.

Ràng buộc

• Có ~20\%~ test có ~k\le 10~;
• Có ~20\%~ test có ~k\le 10^3~;
• Có ~20\%~ test có ~k\le 10^4~;
• Các test còn lại không có ràng buộc gì thêm.

Loli đang là sếp của Bộ phận Hỗ trợ Kỹ thuật cho một công ty IT lớn. Công việc của Loli là đảm bảo tất cả các vấn đề của khách hàng đã được cấp dưới giải quyết.

Hôm nay, Loli kiểm tra bản sao hộp thoại giữa khách hàng và cấp dưới của mình. Theo quy định làm việc, sau mỗi tin nhắn của khách hàng phải có một hoặc vài tin nhắn trả lời của cấp dưới. Tuy nhiên, đôi khi khách hàng đặt câu hỏi nhanh đến mức cấp dưới chưa trả lời xong thì khách đã hỏi thêm.

Để bảo vệ quyền riêng tư, toàn bộ nội dung của tin nhắn bị ẩn, Loli chỉ được xem thứ tự của tin nhắn, cũng như loại của từng tin nhắn: tin nhắn này là câu hỏi của khách hàng hay là tin nhắn trả lời từ cấp dưới. Đảm bảo rằng hộp thoại bắt đầu bằng câu hỏi của khách hàng (vì cấp dưới cần có câu hỏi thì mới trả lời được chứ).

Loli muốn nhờ bạn xác định xem hộp thoại này có hợp lệ với quy cách trên không, hay nó đã bị cắt xén.

Input:

Bài này có nhiều test nhỏ trong một file test, các bạn chú ý.

Lấy từ tệp ITHELP.INP gồm:

• Dòng đầu tiên chứa một số nguyên dương ~T~ là số test nhỏ.
• ~T~ dòng sau, mỗi dòng chứa một xâu ký tự chỉ gồm hai ký tự "Q" và "A", mô tả các loại tin nhắn trong hộp thoại theo thứ tự thời gian. Ký tự "Q" biểu thị tin nhắn có câu hỏi của khách hàng và ký tự "A" biểu thị tin nhắn có câu trả lời của cấp dưới. Đảm bảo rằng ký tự đầu tiên trong xâu bằng "Q".

Output:

Ghi ra tệp ITHELP.OUT gồm:

• ~T~ dòng, dòng thứ ~i~ là đáp án của xâu thứ ~i~. Nếu xâu thứ ~i~ hợp lệ với quy cách, in ra YES, ngược lại in ra NO.

Sample Input 1

4
QQAA
QAA
QQAQ
Q

Sample Output 1

YES
YES
NO
NO

Giải thích

• Ở test nhỏ đầu tiên, hai câu hỏi từ khách hàng được trả lời bởi hai câu trả lời của cấp dưới. Vì vậy, hộp thoại này hợp lệ.
• Ở test nhỏ thứ hai, cấp dưới đã gửi hai tin nhắn dưới dạng câu trả lời cho một tin nhắn duy nhất của khách hàng.
• Ở test nhỏ thứ ba, một trong hai câu hỏi đầu tiên không được trả lời.

Ràng buộc

• ~T \le 100~;
• Có ~30\%~ test có độ dài mọi xâu đều nhỏ hơn ~2000~;
• Các test còn lại có độ dài mọi xâu đều nhỏ hơn ~10^5~.

Một ông già có ~n~ viên kẹo dàn ra trên một đường thẳng, có thứ tự lần lượt từ ~1~ đến ~n~, viên kẹo thứ ~i~ có độ ngon là ~a_i~. Ông già bày thế cho vui thôi, vì ông chỉ cho Loli lấy ~k~ viên kẹo liên tiếp nhau. Thấy kèo không thơm, Loli xin ông già ~k~ lần đổi chỗ 2 viên kẹo bất kỳ, để ít nhất lấy được ~k~ viên kẹo ngon nhất. Tuy nhiên, ông già thấy kèo này hơi OP quá nên ông áp thêm điều kiện là chỉ được đổi chỗ ~2~ viên kẹo có thứ tự lần lượt là ~i~, ~j~ khi và chỉ khi ~i\ mod\ k\ =\ j\ mod\ k~.

Ở đây ~mod~ là phép chia dư, ví dụ ~5\ mod\ 2 = 1~, ~8\ mod\ 3 = 2~.

Loli muốn biết tổng độ ngon tối đa mà mình có thể lấy từ tay ông già.

Input:

Lấy từ tệp MAXCANDY.INP gồm:

• Dòng đầu tiên chứa hai số nguyên dương ~n~ và ~k~ ~(1\le k\le n\le 3\times 10^5)~;
• Dòng thứ hai chứa ~n~ số nguyên không âm ~a_i~ biểu thị độ ngon của viên kẹo thứ ~i~ ~(0\le a_i \le 10^9)~.

Output:

Ghi ra tệp MAXCANDY.OUT gồm:

• Một số nguyên duy nhất là tổng độ ngon tối đa Loli có thể lấy từ tay ông già.

Sample Input 1

3 2
5 6 0

Sample Output 1

11

Sample Input 2

5 3
7 0 4 0 4

Sample Output 2

15

Giải thích

• Ở test đầu tiên, ta có thể chọn ngay viên kẹo thứ ~1~ và ~2~ mà không cần đổi chỗ.
• Ở test thứ hai, ta có thể đổi chỗ viên kẹo thứ ~1~ với viên kẹo thứ ~4~ (vì ~1\ mod\ 3\ =\ 4\ mod\ 3~), sau đó chọn liên tiếp 3 viên kẹo ~3~, ~4~, ~5~.

Ràng buộc

• Có ~20\%~ test có ~n,k\le 100~;
• Có ~20\%~ test có ~n,k\le 10^3~;
• Có ~20\%~ test có ~n,k\le 10^4~;
• Các test còn lại không có ràng buộc gì thêm.

Loli được tham dự một cuộc thi Robot siêu cháy. BTC ra luật chơi như sau:

Robot được đặt ở góc trên cùng bên trái của một lưới các ô gồm ~n~ hàng và ~m~ cột. Góc trên bên trái được định nghĩa là ô ~(1,1)~.

Trong một bước, nó có thể di chuyển tới một ô liền kề với ô ~(i,j)~ hiện tại:

• ~(x,y)→(x,y+1)~;
• ~(x,y)→(x+1,y)~;
• ~(x,y)→(x,y-1)~;
• ~(x,y)→(x-1,y)~.

Robot không thể di chuyển ra ngoài lưới.

Tuy nhiên nếu chỉ có vậy thì quá dễ. BTC quyết định đặt thêm một chùm laser chết chóc. BTC đặt chùm laser đó ở ô ~(s_x,s_y)~. Nếu robot đi vào ô nào đó có khoảng cách nhỏ hơn hoặc bằng ~d~ so với chùm laser, thì robot sẽ bị pay màu.

Khoảng cách giữa hai ô ~(x_1,y_1)~ và ~(x_2,y_2)~ được định nghĩa là ~|x_1-x_2|+|y_1-y_2|~.

Loli muốn biết số bước nhỏ nhất mà robot có thể thực hiện để đi từ ô ~(1,1)~ đến ô ~(n,m)~ mà không bị pay màu hoặc di chuyển ra ngoài lưới. Nếu không thể đến ô ~(n,m)~, hãy in ~-1~.

Chùm laser không ở ô bắt đầu, cũng không ở ô kết thúc. Khoảng cách từ ô xuất phát đến chùm laser luôn lớn hơn ~d~.

Input:

Bài này có nhiều test nhỏ trong một file test, các bạn chú ý.

Lấy từ tệp DEADLASER.INP gồm:

• Dòng đầu tiên chứa một số nguyên dương ~T~ là số test nhỏ (~T\le 10~).
• Có ~T~ test nhỏ, mỗi test nhỏ có cấu trúc như sau:
  • Dòng đầu tiên chứa hai số nguyên ~n, m~ là số hàng và số cột của lưới ~(2\le n,m\le 10^9)~;
  • Dòng thứ hai chứa hai số nguyên ~s_x, s_y~ là tọa độ chùm laser (~1\le s_x \le n,\ 1\le s_y \le m~);
  • Dòng thứ ba chứa số nguyên ~d~, là bán kính hoạt động của chùm laser theo quy cách trên (~0\le d\le n+m~).

Output:

Ghi ra tệp DEADLASER.OUT gồm:

• ~T~ dòng, dòng thứ ~i~ chứa một số nguyên tương ứng với đáp án của test nhỏ thứ ~i~. Nếu không thể đến ô ~(n,m)~, hãy in ~-1~.

Sample Input 1

2
2 3 
1 3 
0
2 3 
1 3 
1

Sample Output 1

3
-1

Sample Input 2

1
5 5 
3 4 
1

Sample Output 2

8

Giải thích

Minh họa test 1.1:

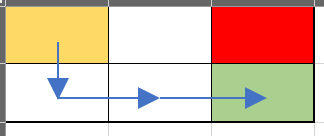
Vùng màu đỏ là vùng hoạt động của chùm Laser. Để đến đích, ta cần đi vòng qua nó. Mất 3 bước để đi tới đích.

Minh họa test 1.2:

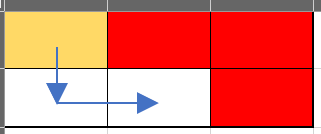
Ta không thể đi đến đích được do nó nằm trong vùng hoạt động của laser.

Minh họa test 2:

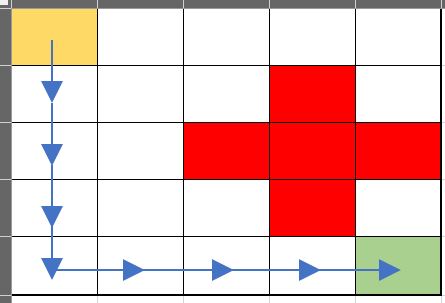
Ràng buộc

• ~1\le T\le 10~.
• Có ~20\%~ test có ~n,m\le 100~;
• Có ~20\%~ test có ~n,m\le 10^3~;
• Có ~20\%~ test có ~n,m\le 10^4~;
• Các test còn lại không có ràng buộc gì thêm.