Trong một tiết học Toán, cô giáo đã cho cả lớp một bài toán khá khoai. Mặc dù chỉ cần dùng não và giấy để giải quyết bài toán, nhưng Loli lại rất thích làm màu. Hắn lôi ra từ trong cặp một chiếc máy tính bàn, một chiếc màn hình ~32~ inch, một chiếc bàn phím cơ và một con chuột gaming lập lòe. Trời ạ, hắn lại định dùng code để giải quyết một bài toán.

Nhanh chóng mở CodeBlocks, hắn nhập "lời giải" cho bài toán như sau:

int n;
double res = 0.0;

int main() {
    cin >> n;
    for(long long i = 1; i <= n; ++i) {
        res = res + 1.0 / (i*(i+1));
    }
    res = (1.0-res)*1000000000;
    cout << fixed << setprecision(6) << res;
}

Với "lời giải" này, hắn tự tin rằng mình sẽ là người giải bài toán đầu tiên của lớp. Tuy nhiên, hắn chờ mãi mà không thấy "lời giải" của mình ghi ra đáp số...

Bạn có thể cải tiến "lời giải" của Loli được không?

Input:

Bài này có nhiều test nhỏ trong một file test, các bạn chú ý.

Lấy từ tệp CAITIEN.INP gồm:

• Dòng đầu tiên chứa một số nguyên dương ~T~ ~(1\le T\le 10^4)~ là số test nhỏ.
• ~T~ dòng sau, mỗi dòng chứa một số nguyên dương ~n~ ~(1 \le n \le 10^9)~ - là đầu vào bài toán của cô giáo.

Output:

Ghi ra tệp CAITIEN.OUT gồm:

• ~T~ dòng, dòng thứ ~i~ chứa một số thực ghi đáp án của test thứ ~i~. Ghi ra ~6~ chữ số phần thập phân.
• Đáp án của bạn được coi là chính xác nếu sai lệch không quá ~10^{-6}~ so với đáp án đúng của cô giáo.

Sample Input 1

3
2
69
177013

Sample Output 1

333333333.333333
14285714.285714
5649.270679

Ràng buộc

• Có ~50\%~ test có ~T\times n \le 10^8~;
• Các test còn lại không có ràng buộc gì thêm.

Loli đang triển khai một đội hình đặc nhiệm để chuẩn bị cho kế hoạch tiếp theo. Trong lúc kiểm tra lại đội hình một lần cuối, Loli nhận ra có gì đó sai sai. Trong đội hình toàn đặc nhiệm cao đều răm rắp, có một chỗ lại bị thò thụt bất thường, và chỉ có một chỗ bị như vậy.

Loli báo cáo lại cho cấp dưới. Cấp dưới không tin có chuyện đó xảy ra. Tuy nhiên, với cách suy nghĩ "Đúng nhận sai cãi", cấp dưới truyền lệnh cho đội hình đặc nhiệm dàn ra thành một hàng ngang, đánh số từng người lần lượt từ ~1~ đến ~n~, sau đó sử dụng một máy đo chuyên dụng để biết độ cao của từng người.

Công việc còn lại của Loli là code chương trình để tìm ra được kẻ giả mạo đó. Nhưng Loli lười code nên giao trọng trách lại cho bạn. Bạn hãy xác định xem Cấp dưới sẽ phải nhận hay được cãi. Nếu đúng có kẻ giả mạo, hãy cho biết số thứ tự của kẻ đó.

Input:

Lấy từ tệp IMPOSTOR.INP gồm:

• Dòng đầu tiên chứa một số nguyên dương ~n~ ~(3\le n\le 10^5)~ là số người.
• Dòng tiếp theo chứa ~n~ số nguyên dương ~a_i~ ~(1\le a_i \le 10^9)~ là chiều cao của đặc nhiệm có số thứ tự ~i~.

Output:

Ghi ra tệp IMPOSTOR.OUT gồm:

• Dòng thứ nhất ghi kết quả cuộc điều tra. Nếu tất cả đều có chiều cao bình thường, in ra YES, ngược lại, in ra NO.
• Dòng thứ hai ghi một số nguyên là số thứ tự của kẻ giả mạo, nếu có. Nếu không có kẻ giả mạo nào, in ra ~-1~ ở dòng này.

Sample Input 1

4
11 11 13 11

Sample Output 1

NO
3

Trong lúc làm bài căng thẳng, cần một bài toán để phá tan sự căng thẳng đó!!

Trong contest lần này, bạn có muốn được giải thưởng không?

Input:

Lấy từ tệp IWANT.INP gồm:

• Dòng đầu tiên chứa một số nguyên dương ~n~ ~(1\le n\le 100)~.

Output:

Ghi ra tệp IWANT.OUT gồm:

• In ra dòng chữ "l want" và ~n~ dấu chấm than ở đằng sau.

Sample Input 1

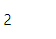
Sample Output 1

Loli đang chơi Arknights. Trong màn chơi hiện tại, Loli cần phải tiêu diệt ~n~ con quái, con quái thứ ~i~ có ~h_i~ điểm HP.

Nhân vật duy nhất đang gánh còng lưng Loli có hai kỹ năng:

• Chọn hai con quái đang sống và tấn công đồng thời hai bọn chúng, khiến mỗi con quái bị trừ ~1~ điểm HP.
• Chọn một con quái rồi dùng nội tại để tiêu diệt nó ngay lập tức.

Hai kỹ năng có thể được thực hiện vô hạn lần, với thứ tự thực hiện bất kỳ. Trong một đơn vị thời gian, Loli có thể sử dụng một trong hai kỹ năng đó.

Khi con quái có điểm HP về ~0~, nó sẽ bị tiêu diệt.

Tuy nhiên, Loli sắp bị mẹ gank. Vì vậy, Loli muốn biết hắn có thể quét sạch quái trong thời gian nhanh nhất là bao lâu.

Input:

Bài này có nhiều test nhỏ trong một file test, các bạn chú ý.

Lấy từ tệp DANHQUAI.INP gồm:

• Dòng đầu tiên chứa một số nguyên dương ~T~ ~(1\le T\le 500)~ là số test nhỏ.
• Có ~T~ test nhỏ, mỗi test nhỏ có cấu trúc như sau:
  • Dòng đầu tiên chứa một số nguyên dương ~n~ ~(1 \le n \le 10^5)~ - là số lượng quái cần đánh.
  • Dòng tiếp theo chứa ~n~ số nguyên dương ~h_i~ ~(1 \le h_i \le 100)~ là điểm HP của con quái thứ ~i~.

Output:

Ghi ra tệp DANHQUAI.OUT gồm:

• ~T~ dòng, dòng thứ ~i~ chứa một số nguyên tương ứng với đáp án của test nhỏ thứ ~i~.

Sample Input 1

3
4
2 1 1 2
3
4 2 2
5
1 2 3 5 8

Sample Output 1

3
3
5

Giải thích

• Ở test đầu tiên, có nhiều cách để tiêu diệt toàn bộ quái trong ~3~ đơn vị thời gian. Một cách đánh là:
  • Dùng kỹ năng thứ nhất lên con quái thứ ~1~ và ~2~. Quái thứ ~1~ còn ~1~ HP, quái thứ ~2~ bị tiêu diệt. Mảng còn lại là ~[1,0,1,2]~.
  • Dùng kỹ năng thứ nhất lên con quái thứ ~3~ và ~4~. Quái thứ ~4~ còn ~1~ HP, quái thứ ~3~ bị tiêu diệt. Mảng còn lại là ~[1,0,0,1]~.
  • Dùng kỹ năng thứ nhất lên con quái thứ ~1~ và ~4~. Cả hai con quái đều bị tiêu diệt.
• Ở test thứ hai, một cách đánh là:
  • Dùng kỹ năng thứ nhất lên con quái thứ ~2~ và ~3~. Cả hai con quái đều còn ~1~ HP. Mảng còn lại là ~[4,1,1]~.
  • Dùng kỹ năng thứ nhất lên con quái thứ ~2~ và ~3~. Cả hai con quái đều bị tiêu diệt. Mảng còn lại là ~[4,0,0]~.
  • Dùng kỹ năng thứ hai lên con quái thứ ~1~. Quái thứ ~1~ bị tiêu diệt.

Chủ đề vẫn là con game Arknights mà Loli đang chơi.

Arknights có rất nhiều màn chơi. Ta có thể đơn giản hóa rằng, tựa game này có ~n~ màn chơi tất cả. Mỗi màn chơi sẽ yêu cầu người chơi phải có cấp độ không dưới cấp độ mà màn chơi yêu cầu. Gọi cấp độ tối thiểu để chơi màn chơi thứ ~i~ là ~h_i~.

Các màn chơi sẽ càng ngày càng khó, đòi hỏi người chơi phải có cấp độ càng ngày càng cao. Nói cách khác, ta có ~h_i \le h_{i+1}~ với mọi ~i < n~.

Do Loli rất yêu tựa game này nên Loli lập ra ~q~ tài khoản, mỗi tài khoản được đánh số thứ tự từ ~1~ đến ~q~. Hiện tại cấp độ tài khoản thứ ~i~ của Loli là ~x_i~, và Loli muốn biết rằng, nếu hắn cố gắng lên thêm ~y_i~ cấp độ nữa ở tài khoản này, thì hắn sẽ qua được thêm bao nhiêu màn chơi?

Input

Lấy từ tệp THANGCAP.INP gồm:

• Dòng đầu tiên chứa một số nguyên dương ~n~ ~(1\le n\le 5\times 10^5)~ là số màn chơi.
• Dòng thứ hai chứa ~n~ số nguyên dương ~h_i~ ~(1\le h_i\le 2\times 10^9)~ là cấp độ tối thiểu để chơi màn chơi thứ ~i~.
• Dòng thứ ba chứa số nguyên dương ~q~ ~(1\le q \le 10^5)~ là số tài khoản của Loli.
• ~q~ dòng tiếp theo, mỗi dòng chứa hai số nguyên dương ~x_i~ và ~y_i~ ~(1\le x_i, y_i \le 10^9)~ thể hiện câu hỏi của Loli ở tài khoản thứ ~i~.

Output

Ghi ra tệp THANGCAP.OUT gồm:

• ~q~ dòng, dòng thứ ~i~ chứa một số nguyên tương ứng với số màn chơi có thể qua được thêm sau khi thăng cấp ở tài khoản thứ ~i~.

Sample Input 1

5
2 6 7 10 15
3
1 3
7 8
5 20

Sample Output 1

1
2
4

Giải thích

• Ở tài khoản thứ ~1~, Loli thăng cấp từ cấp ~1~ lên cấp ~1+3=4~, qua thêm được màn chơi thứ ~1~.
• Ở tài khoản thứ ~2~, Loli thăng cấp từ cấp ~7~ lên cấp ~7+8=15~, qua thêm được ~2~ màn chơi là màn thứ ~4~ và ~5~.
• Ở tài khoản thứ ~3~, Loli thăng cấp từ cấp ~5~ lên cấp ~5+20=25~, qua thêm được ~4~ màn chơi từ màn thứ ~2~ đến màn thứ ~5~.

Ràng buộc

• ~40\%~ test có ~q\times n \le 10^8~;
• ~60\%~ test còn lại không có ràng buộc gì thêm.

Trong khu vườn, người ta trồng một hàng cây chạy dài gồm có ~N~ cây, mỗi cây có độ cao là ~a_1, a_2, \dots, a_N~. Người ta cần lấy ~M~ mét gỗ bằng cách đặt cưa máy sao cho lưỡi cưa ở độ cao ~H~ (mét) để cưa tất cả các cây có độ cao lớn hơn ~H~ (dĩ nhiên những cây có độ cao không lớn hơn ~H~ thì không bị cưa).

Ví dụ: Nếu hàng cây có các cây với độ cao tương ứng là ~20; 15; 10; 18~ mét, cần lấy ~7~ mét gỗ. Lưỡi cưa đặt tại độ cao hợp lí là ~15~ mét thì độ cao của các cây còn lại sau khi bị cưa tương ứng là ~15; 15; 10; 15~ mét. Tổng số mét gỗ lấy được là ~8~ mét (dư ~1~ mét).

Yêu cầu: Hãy tìm vị trí đặt lưỡi cưa hợp lí (số nguyên ~H~ lớn nhất) sao cho lấy được ~M~ mét gỗ và số mét gỗ dư ra là ít nhất.

Input:

File "WOOD.INP" gồm:

• Dòng thứ nhất chứa ~2~ số nguyên dương ~N~ và ~M~ ~(1 \le N \le 10^6;\ 1 \le M \le 2 \times 10^9)~ cách nhau một dấu cách.
• Dòng thứ hai chứa ~N~ số nguyên dương ~a_i~ là độ cao của mỗi cây trong hàng ~(1 \le a_i \le 10^9\; i=1 \dots N)~, mỗi số cách nhau ít nhất một dấu cách.

Output:

• File "WOOD.OUT" một số nguyên cho biết giá trị cần tìm.

Sample Input 1

4 7
20 15 10 18

Sample Output 1

15