Loli Academy 2023 Contest 0001 - Số học & Tổ hợp
Điểm: 20

Điểm: 20
Số chính phương là bình phương của một số nguyên. Ví dụ, ~1 = 1^2~, ~4870849 = 2207^2~ và ~31393609 = 5603^2~ là các số chính phương, còn ~2~, ~8~ hay ~10~ thì không. Trong bài toán này, ta chỉ xét các số chính phương là bình phương của một số nguyên dương.
Ta gọi một số là số chính phương không lặp lại khi và chỉ khi số đó là số chính phương và trong biểu diễn của số đó trong hệ thập phân, không có chữ số nào xuất hiện nhiều hơn một lần. Ví dụ, ~25 = 5^2~, ~36 = 6^2~ và ~49 = 7^2~ là các số chính phương không lặp lại, còn ~100 = 10^2~, ~121 = 11^2~ và ~144 = 12^2~ thì không (vì có các chữ số ~0~, ~1~ hay ~4~ xuất hiện nhiều hơn một lần).
Ta viết các số chính phương không lặp lại dương thành một dãy và sắp xếp chúng theo thứ tự tăng dần, ta được dãy ~1, 4, 9, \dots~
Yêu cầu: Cho một số nguyên dương ~k~, hãy tìm số thứ ~k~ trong dãy.
Input:
- Một số nguyên duy nhất ~k~ ~(1 \le k \le 10^{18})~.
Output:
- Một số nguyên là số chính phương không lặp lại lớn thứ ~k~. Nếu số này không tồn tại, in ra ~-1~.
Sample Input 1
9
Sample Output 1
81
Sample Input 2
10
Sample Output 1
169
Một ông già rảnh hơi nào đó đã viết cho Loli ~Q~ số nguyên và bảo Loli phải kiểm tra xem số đó có phải là số nguyên tố không. Nếu Loli trả lời đúng hết thì ông già sẽ mời Loli về nhà riêng của mình…
Input:
Vào từ file văn bản NTO.INP gồm:
- Dòng ~1~: chứa số nguyên dương ~Q~ ~(1 \le Q \le 10^5)~.
- Dòng ~2~ đến dòng ~Q+1~: dòng ~i+1~ chứa số nguyên ~a[i]~ cần kiểm tra ~(|a[i]| \le 10^6)~.
Output:
Ghi ra file văn bản NTO.OUT gồm:
- ~Q~ dòng, dòng ~i~ là kết quả kiểm tra tính nguyên tố của số nguyên ~a[i]~. Nếu không là số nguyên tố, in ra
Yes, ngược lại, in raNo.
Ví dụ:
NTO.INP
1
3
NTO.OUT
No
Điểm: 20
Mọi người dân vô tội đang phải chịu một điều luật hà khắc do Loli rảnh rỗi sinh nông nổi tạo ra, có tên là CLGT. Bộ luật đã thay đổi hoàn toàn cách người dân tính toán các số. Ở bài toán này các bạn cần tìm "cội nguồn" của một số. Theo điều luật CLGT, "cội nguồn" là tổng các chữ số của một số nguyên, lấy số đó tính đi tính lại cho tới khi nó trở thành số có một chữ số.
Input:
- Một số nguyên dương ~N~ duy nhất ~(1 \le N \le 10^{18})~.
Output:
- Một số nguyên dương là đáp án của bài toán.
Sample Input 1
1
Sample Output 1
1
Sample Input 2
81
Sample Output 2
9
Sample Input 3
1624
Sample Output 3
4
Giải thích
- Ở test 1, cách biến đổi sẽ là: ~1 \rightarrow 1~.
- Ở test 2, cách biến đổi sẽ là: ~81 \rightarrow 9~.
- Ở test 3, cách biến đổi sẽ là: ~1624 \rightarrow 13 \rightarrow 4~.
Điểm: 20
Dạo một vòng Facebook, Loli cảm thấy rất chán khi thấy giới trẻ cứ thấy cái gì đấy là lại muốn "uoc j uoc j". Vì vậy Loli nhờ các bạn coder giải quyết vấn nạn nhức nhối này bằng việc tạo ra chương trình trả lời hết các câu "uoc j".
Input:
- Dòng đầu tiên chứa một số nguyên ~j~ ~(1 \le j \le 10^{12})~.
Output:
- Gồm một dãy số nguyên tăng dần là ước của ~j~.
Sample Input 1
3
Sample Output 1
1 3
Sample Input 2
69
Sample Output 2
1 3 23 69
Nam là một người mới bắt đầu học lập trình. Hôm nay Nam học về mảng. Anh ấy có một mảng ~n~ số nguyên dương là ~a_1, a_2, \dots, a_n~. Giáo viên của anh cho một nhiệm vụ, tìm một số ~x~ trong mảng thoả mãn: tất cả các số khác trong mảng đều chia hết cho số ~x~ đó. Hãy giúp anh ấy tìm ra số ~x~ đó!
Input:
File "SNUM.INP" gồm:
- Dòng đầu chứa số nguyên ~n\ (1\le n \le 10^5)~, cho biết số lượng số nguyên dương trong mảng.
- Dòng thứ hai gồm các số nguyên ~a_1, a_2, \dots, a_n\ (1 \le a_i \le 10^9)~, là các phần tử của mảng.
Output:
File "SNUM.OUT":
- Ghi một số nguyên ~x~ duy nhất, sao cho tất cả các số khác trong mảng đều chia hết cho số ~x~ đó.
- Nếu số đó không tồn tại, đưa ra ~-1~.
Ví dụ 1:
SNUM.INP
3
2 2 4
SNUM.OUT
2
Ví dụ 2:
SNUM.INP
5
2 1 3 1 6
SNUM.OUT
1
Ví dụ 3:
SNUM.INP
3
2 3 5
SNUM.OUT
-1
Điểm: 25
Chàng sinh viên IT trẻ thấy một cậu bé cấp II đang cúp học chơi net, chàng ta liền tiến lại bắt chuyện.
- Mai mốt lớn lên, em muốn làm gì?
- Em thích game lắm, lớn lên em sẽ làm game ạ!
- Thế em biết làm game cần những cái gì không?
- Tất nhiên là có rồi. Đó chính là đam mê với máy tính!
Chàng sinh viên lặng người. Những ký ức ác mộng về quá trình sản xuất game độc lập. Nào là thuật toán, nào là thiết kế đồ họa, thiết kế giao diện người dùng, sản xuất nhạc, tối ưu hóa, vật lý cao cấp, toán cao cấp, lập trình, ... cứ thế chạy qua trong tâm trí của anh.
Anh nhớ lại, đã có một thời mình cũng từng ngây thơ như vậy, đôi mắt của mình cũng từng sáng như cậu bé này, sự nhiệt huyết tuổi trẻ mà anh đã đánh mất. Tất cả điều đó khiến mắt anh nhòe đi. Giờ đây nhìn lại mình. Chàng sinh viên thấy mình đã già, mắt đã cận, lưng còng, đít trĩ, tay run.
"Không, không thể như thế được! Mình phải bảo vệ đôi mắt ngây thơ này!".
Thế là anh đè cậu bé ra đấm túi bụi, vừa đấm vừa chửi:
- Á à, cúp học chơi gêm còn bày đặt lày! Láo này! Học không lo học suốt ngày gêm!
*bốp *bốp *bốp
Cậu bé vừa xách quần chạy vừa chửi thầm trong đầu. Còn anh sinh viên thì nấp sau góc tường, ngồi phệt xuống sàn và suy nghĩ câu hỏi sau: "Cho một số nguyên dương ~N~. Tìm số nhỏ nhất chỉ gồm chữ số ~1~ chia hết cho ~N~".
Input:
- Gồm một số nguyên dương ~N~ ~(1 \le N \le 2 \times 10^6)~.
Output:
- Gồm một số nguyên dương là số cần tìm. Nếu không có kết quả in ra ~-1~. Nếu có kết quả, đề bài đảm bảo kết quả không vượt quá ~10^{10^7}~.
Subtasks:
- ~20\%~ số test không có kết quả hoặc có kết quả không vượt quá ~10^7~.
- ~20\%~ số test có kết quả không vượt quá ~10^{18}~.
- ~30\%~ số test có kết quả không vượt quá ~10^{727}~.
- ~30\%~ số test không có ràng buộc gì thêm.
Sample Input 1
69
Sample Output 1
111111111111111111111111111111111111111111111111111111111111111111
Sample Input 2
420
Sample Output 2
-1
Giải thích:
- Ở test 1, ~111111111111111111111111111111111111111111111111111111111111111111/69 = 1610305958132045088566827697262479871175523349436392914653784219~ và dư ~0~.
- Ở test 2, một số chia hết cho ~420~ luôn kết thúc bằng chữ số ~0~, nhưng nó là điều bất khả thi vì số toàn ~1~, như việc tôi có người yêu vậy…
Điểm: 30
Tôi chẳng biết trong đầu em đang nghĩ gì... Xung quanh em có quá nhiều người bạn, cũng thừa những người theo đuổi em... Khi mọi người đã ngủ say, và có lẽ cả em cũng vậy, tôi lại tự hỏi rằng liệu em có đang mơ về ai kia, hay tôi lại may mắn được làm ai kia trong giấc mơ của em?
Mơ... Gặp được em đã là một trong những thứ điên tới mức tôi chẳng bao giờ mơ về, đặc biệt với một người mà ai ai cũng biết tới. Thậm chí ngay từ đầu tại sao tôi lại gặp được em cơ chứ? Và có lẽ tài năng như em thì tôi làm gì có cơ hội?
Ai biết được nhỉ? Điều tôi biết duy nhất là bây giờ, sâu trong giấc ngủ em đang mơ về ai đó, trong khi tôi đang mơ về một thuật toán đúng để giải bài toán sau đây:
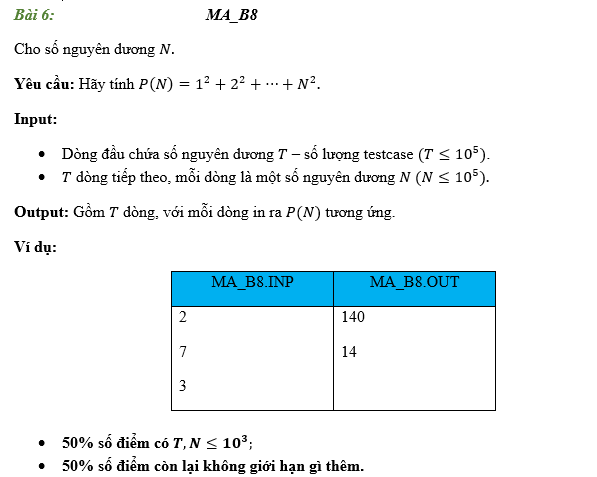
Cho số nguyên dương ~N~, hãy tính ~S = 1 \cdot 2 + 2 \cdot 3 + 3 \cdot 4 + \dots + N(N+1)~.
Input:
- Gồm một số nguyên dương ~N\ (1 \le N \le 10^9)~.
Output:
- Gồm một số nguyên dương là số dư của ~S~ trong phép chia cho ~177013~.
Sample Input
3
Sample Output
20
Giải thích
Ta có: ~S=1 \cdot 2+2 \cdot 3+3 \cdot 4=20~.
Ràng buộc
- 50% số test có ~N \le 10^4~.
- 30% số test có ~N \le 10^7~.
- 20% số test không có ràng buộc gì thêm.
Nam làm nghề thợ xây. Anh có ~n~ viên gạch được đánh số từ ~1~ tới ~n~. Nhiệm vụ của anh là phải sơn những viên gạch này. Một viên gạch sẽ được sơn màu đỏ nếu chỉ số của nó chia hết cho ~a~. Một viên gạch sẽ được sơn màu xanh da trời nếu chỉ số của nó chia hết cho ~b~. Viên gạch mà chỉ số của nó đều chia hết cho ~a~ và ~b~ có thể được sơn màu đỏ hoặc màu xanh da trời.
Sau khi sơn gạch, Nam sẽ nhận được ~p~ miếng sô cô la cho mỗi viên gạch sơn màu đỏ và ~q~ miếng sô cô la cho mỗi viên gạch sơn màu xanh.
Lưu ý rằng Nam có thể sơn gạch theo bất kỳ thứ tự nào anh ấy muốn. Tìm số lượng sô cô la lớn nhất Nam có thể nhận.
Input:
- File "PAINT.INP" gồm một dòng duy nhất chứa ~5~ số nguyên ~n, a, b, p~ và ~q~ ~(1 \le n,a,b,p,q \le 10^9)~
Output:
- File "PAINT.OUT" ghi duy nhất số nguyên ~s~ là số miếng sô cô la lớn nhất mà Nam có thể nhận.
Sample Input 1
5 2 3 12 15
Sample Output 1
39
Sample Input 2
20 2 3 3 5
Sample Output 2
51
Điểm: 30
Trong trường hợp đề bài hiển thị không chính xác, bạn có thể tải đề bài tại đây: Đề bài
Điểm: 10
Con mèo dí súng vào đầu con chó rồi hỏi:
- 1+1 = mấy?
- Dạ! = 2 ạ!
'Pằng', con mèo thổi khói súng: Mày đã biết quá nhiều.
Vẫn câu hỏi đó, con chó thứ 2 suy nghĩ rồi run rẩy trả lời:
- Dạ! em không biết ạ!
'Pằng', con mèo lại thổi khói: Loại dốt nát như mày không nên sống.
Đến con chó thứ 3, mèo vẫn hỏi lại câu hỏi đó. Con này suy nghĩ rồi trả lời:
- Biết thì sao mà không biết thì sao?
'Pằng'!: Nguy hiểm như mày thì càng phải chết.
Tiếp tục con chó thứ 4, lại là câu hỏi đó, con này suy nghĩ rồi trả lời:
- Trả lời anh giết, không trả lời anh giết, trả lời sai anh giết, trả lời đúng cũng giết luôn, thì em biết phải làm sao?
'Pằng'!: Mày phải chết vì mày nói quá nhiều.
Đến con cuối cùng, vẫn câu hỏi cũ, con này nhanh nhảu trả lời:
- Dạ thưa anh! Với những câu hỏi hóc búa như vậy, thì chỉ có những người cao siêu như anh mới có đáp án chính xác ạ!
Con mèo khoái chí bảo: Mày được, theo tao!
Yêu cầu: Theo bạn, ~1+1\ =\ ?~
Input:
- Không có Input.
Output:
- Đáp án cần tìm.
Điểm: 100
VOZ là một diễn đàn lớn tại Việt Nam, nơi các thành viên có thể trao đổi về những chủ đề trong lĩnh vực CNTT. Ngoài CNTT, VOZ còn là nơi ươm mầm tài năng có tiếng, những người đã từng đặt chân đến mảnh đất này gọi là VOZer. Một hôm, admin VOZ có mở một contest cho những VOZer. Trong contest này, mọi VOZer làm mọi cách để chứng tỏ mình là một Winner chứ không phải là một Lesor 200 chap. Sau hai tuần cưa gái vất vả, ban tổ chức công bố bảng điểm tổng cho toàn thể thiên hạ. Thứ hạng của một VOZer chính là số lượng VOZer khác có điểm lớn hơn người này rồi cộng thêm ~1~. Bên dưới là BXH minh họa:
| Thứ hạng | Thí sinh | Độ Winner Chất chơi Người dơi |
|---|---|---|
| 1 | Hoài Linh | 14000000000 |
| 2 | Sena | 3300000000 |
| 3 | Đạt Villa | 400000000 |
| 4 | Jack 97 | 5000000 |
| 4 | Mèo Simmy | 5000000 |
| 6 | Người ra đề | 0 |
Chỉ cần nhìn vào cột "Thứ hạng", ta có thể thấy giá trị trong cột này tạo thành một dãy không giảm gồm ~n~ phần tử, ngoài ra còn có nhiều tính chất thú vị khác. Nhiệm vụ của bạn là đếm toàn bộ số dãy Thứ hạng có thể. Chú ý rằng dãy ~A~ và ~B~ được coi là khác nhau khi tồn tại một vị trí ~i~ trong dãy mà ~A_i \neq B_i~.
Input:
- Gồm một số nguyên dương ~n\ (1 \le n \le 2 \times 10^9)~.
Output:
- Gồm một số nguyên dương là số dãy có thể tạo ra sau khi chia dư cho ~10^9+7~.
Sample Input
3
Sample Output
4
Giải thích
Có ~4~ dãy xếp hạng có thể:
- 1 1 1: Ba VOZer ngang điểm.
- 1 1 3: Hai VOZer đứng đầu bằng điểm và hơn VOZer thứ 3.
- 1 2 2: Một VOZer xuất chúng, 2 VOZer còn lại bằng điểm.
- 1 2 3: Ba VOZer có điểm khác nhau.
Ràng buộc
- 30% số test có ~n \le 10~.
- 20% số test có ~n \le 10^4~.
- 30% số test có ~n \le 10^7~.
- 20% số test không có ràng buộc gì thêm.
Điểm: 100
Sau khi mua quá nhiều sách, Loli muốn chia sẻ lại niềm vui đọc sách đến đám bạn của hắn. Hãy giúp Loli tính nhanh số cách chia ~n~ quyển sách cho ~k~ người bạn (tất nhiên có thể có người không nhận được sách, tuy nhiên cần đảm bảo quyển sách nào cũng được chia).
Hai cách chia được coi là khác nhau nếu tồn tại ~i~ sao cho người thứ ~i~ nhận được số sách khác nhau ở trong 2 cách chia. Bạn chỉ cần in ra phần dư khi chia cho ~10^9+7~.
Input:
Lấy từ tệp DIVBOOK.INP:
- Dòng đầu tiên chứa số nguyên ~q\ (q\le100)~ là số truy vấn cần tính.
- ~q~ dòng tiếp theo, mỗi dòng chứa hai số nguyên ~n,k\ (1\le n,k\le10^7)~.
Output:
Ghi ra tệp DIVBOOK.OUT:
- Gồm ~q~ dòng, mỗi dòng chứa phần dư của số cách chia khi chia cho ~10^9+7~.
Sample Input 1
1
3 2
Sample Output 1
4
Giải thích
Có ~4~ cách chia tất cả:
- Người 1 có ~0~ quyển sách, người 2 có ~3~ quyển.
- Người 1 có ~1~ quyển sách, người 2 có ~2~ quyển.
- Người 1 có ~2~ quyển sách, người 2 có ~1~ quyển.
- Người 1 có ~3~ quyển sách, người 2 có ~0~ quyển.
Ràng buộc
- 30% số test có ~n,k\le20~.
- 30% số test có ~n,k\le10^3~.
- 40% số test không có ràng buộc gì thêm.
Cho một thùng nước và hai gáo nước có dung tích lần lượt là ~A~ và ~B~. Ban đầu thùng nước rỗng. Một người phải dùng hai gáo nước múc nước vào thùng với điều kiện khi múc vào hay múc ra đều phải đong đầy gáo. Hãy tìm cách dùng số lần múc nước ít nhất để có được lượng nước là ~C~ trong thùng.
Input:
- Dòng đầu chứa số ~k \le 100~ là số test;
- ~k~ dòng tiếp theo, mỗi dòng chứa ba số nguyên dương ~A, B, C \le 10^9~ cách nhau bởi dấu cách tương ứng với một test.
Output:
- Ứng với mỗi test, ghi ra trên một dòng một số nguyên duy nhất là số lần múc theo phương án tìm được, nếu không thể thực hiện yêu cầu ghi ra số ~-1~.
Sample Input 1
2
15 24 3
100 27 8
Sample Output 1
5
5
Tính điểm:
- Test case ~1~: Dùng gáo ~24~ múc vào ~2~ lần và dùng gáo ~15~ đổ ra ~3~ lần;
- Test case ~2~: Dùng gáo ~27~ múc vào ~4~ lần và dùng gáo ~100~ múc ra ~1~ lần.
Điểm: 100
Một robot thử nghiệm đang ở gốc tọa độ ~(0,0)~. Mỗi bước di chuyển, từ ô ~(x,y)~ robot có thể di chuyển đến một trong ba vị trí ~(x+1,y),\ (x,y+1),\ (x+1,y+1)~. Hãy đếm số cách đi khác nhau để robot có thể đi đến được vị trí ~(m,n)~. Hai cách đi được coi là khác nhau nếu số bước di chuyển khác nhau hoặc số bước di chuyển bằng nhau và tồn tại một số nguyên ~i~ sao cho bước di chuyển thứ ~i~ ở hai cách đi là khác nhau.
Input
- Gồm một dòng duy nhất chứa hai số nguyên ~m,n~ (~1 \le m,n \le 10^7~).
Output
- Một số nguyên duy nhất là số cách đi khác nhau của robot. Do con số này có thể rất lớn nên bạn chỉ cần in ra phần dư của nó khi chia cho ~10^9+7~.
Sample Input 1
3 3
Sample Output 1
63
Điểm: 100
Hãy tính số lượng tập con có ~k~ phần tử của ~\{1, 2, ..., n\}~. Do con số này quá lớn nên bạn chỉ cần lấy phần dư của nó khi chia cho ~m~.
Input:
- Dòng đầu tiên chứa số nguyên dương ~T~ (~T\le 100~) - số lượng bộ dữ liệu.
- ~T~ dòng tiếp theo, mỗi dòng chứa ba số ~n, k, m~ (~1\le n \le 10^5; 0\le k\le n~, ~2\le m \le 10^9~).
Output:
- In ra ~T~ dòng tương ứng với kết quả các bộ dữ liệu (theo thứ tự trong input).
Sample Input 1
5
11 11 100
14 10 1000
14 4 10000
13 0 100000
12 11 1000000
Sample Output 1
1
1
1001
1
12
Điểm: 100
Cho ba số nguyên dương ~a, b, c~. Xét phương trình: ~ax + by = c~
Yêu cầu: Tìm số lượng cặp ~(x, y)~ là nghiệm của phương trình với ~x, y~ là hai số nguyên dương.
Input
- Một dòng chứa ba số nguyên dương ~a, b, c\ (a, b,c \le 10^9)~.
Output
- Một số nguyên duy nhất là số lượng cặp nghiệm nguyên dương của phương trình.
Sample Input 1
2 4 20
Sample Output 1
4
Sample Input 2
6 12 1800
Sample Output 2
149
Test 1, có 4 cặp nghiệm: ~2\times 2+4\times 4=20~, ~2\times 4+4\times 3=20~, ~2\times 6+4\times 2=20~, ~2\times 8+4\times 1=20~
Điểm: 100
Bờm rất yêu thích môn toán. Vừa rồi Bờm được nghe bài giảng về ước số chung lớn nhất (viết tắt là ~gcd~) và bội số chung nhỏ nhất (~lcm~). Ước số chung lớn nhất của hai số nguyên dương ~a~ và ~b~, ký hiệu ~gcd(a,b)~ là số nguyên lớn nhất mà ~a~ và ~b~ đều chia hết cho số đó. Tương tự, bội số chung nhỏ nhất của hai số nguyên dương ~a~ và ~b~, ký hiệu ~lcm(a,b)~ là số nguyên nhỏ nhất chia hết cho cả ~a~ và ~b~.
Bờm nhận thấy có thể có các cặp số mà ~gcd~ và ~lcm~ là như nhau. Bờm mới nghĩ ra bài toán sau: Cho hai số nguyên dương ~a, b~, trong số các cặp số ~(x,y)\ (1\le x \le y)~ có cùng ~gcd~ và ~lcm~ như cặp ~(x,y)~, hãy tìm cặp ~(x,y)~ thỏa mãn sao cho hiệu ~y-x~ là nhỏ nhất.
Input
- Một dòng chứa hai số nguyên dương ~a, b\ (1\le a,b\le 10^9)~.
Output
- Ghi hai số nguyên ~x~ và ~y~ ~(1\le x \le y)~ tìm được theo yêu cầu.
Sample Input 1
3 4
Sample Output 1
3 4
Sample Input 2
1 12
Sample Output 2
3 4
Sample Input 3
720 1007
Sample Output 3
848 855
Điểm: 100
Cho tập ~A~={~a_1,a_2,\dots,a_n~}. Đếm số lượng số nguyên dương không vượt quá ~K~ thỏa mãn:
~a~ - Chia hết cho ít nhất một trong các số thuộc tập ~A~
~b~ - Chia hết cho duy nhất một số thuộc tập ~A~
Input
- Dòng đầu chứa hai số nguyên dương ~n,k\ (n≤20,k≤10^{18})~
- Dòng thứ 2 chứa ~n~ số nguyên dương ~a_1,a_2,\dots,a_n~ (~a_i≤10^9~).
Output
- Ghi 2 số nguyên lần lượt là đáp án cho 2 câu hỏi ~a~, ~b~.
Sample Input 1
3 10
3 5 2
Sample Output 1
8 6
Subtask
- ~50\%~ số test có ~k\le 10^6~.
- ~50\%~ số test có ~k\le 10^{18}~.
Hãy đếm xem có bao nhiêu mảng khác nhau ~a_1, a_2, \dots, a_n~ trong đó ~a_i~ nhận các giá trị nguyên dương trong đoạn ~[1,M]~ sao cho tồn tại ít nhất một đoạn ~K~ giá trị liên tiếp giống nhau?
Ở đây hai mảng được gọi là khác nhau nếu như tồn tại ít nhất một vị trí mà giá trị phần tử hai mảng ở vị trí này là khác nhau.
Input
- Một dòng duy nhất chứa ba số nguyên dương ~n,M,K\ (1\le n,M,K\le 10^6)~.
Output
- Một số nguyên duy nhất là số lượng mảng khác nhau tìm được. Con số này có thể rất lớn nên bạn chỉ cần lấy phần dư của nó khi chia cho ~10^9+7~.
Sample Input 1
3 2 2
Sample Output 1
6
Giải thích: Các mảng tìm được là ~(1, 1, 1), (1, 1, 2), (1, 2, 2), (2, 1, 1), (2, 2, 1), (2, 2, 2)~.
Điểm: 200
Cho một dãy số nguyên dương ~a~ gồm ~n~ phần tử. Bạn cần chỉ ra có tồn tại số nguyên dương ~x~ sao cho ~gcd(a_i + x, a_j + x) = 1~ với mọi ~1≤i<j≤n~.</p>
Bài toán gồm nhiều test case, mỗi trường hợp bạn cần trả ra "YES" hoặc "NO" tương ứng với việc tồn tại ~x~ hay không.
Input:
- Dòng đầu chứa ~t\ (1≤t≤100)~ số lượng test case. Với mỗi test case:
- Dòng đầu chứa ~2 ≤ N ≤ 100~, số lượng phần tử.
- Dòng tiếp theo chứa ~N~ số ~a_1, a_2, \dots, a_N\ (1≤a_i≤10^{18})~.
Output:
- Đưa ra "YES" hoặc "NO" cho từng trường hợp.
Sample Input 1
2
3
5 7 10
3
3 3 4
Sample Output 1
YES
NO
Subtask
- 25% số điểm có ~N \le 10;\ a_i \le 1000~;
- 25% số điểm có ~a_i \le 10^9~;
- 50% số điểm không có ràng buộc gì thêm.
Điểm: 200

Ràng buộc

Sample Input 1
1 10
Sample Output 1
4
Sample Input 2
2 100
Sample Output 2
273
Sample Input 3
8 10
Sample Output 3
51145857
Điểm: 200
Note: Test yêu cầu tìm vị trí tính sau dấu chấm thập phân, đề bài diễn tả không đúng. Nói cách khác, ~S~ chỉ bao gồm phần thập phân, các bạn lưu ý.

Sample Input 1
3 7 2
2
Sample Output 1
8
Sample Input 2
3 5 2
00
Sample Output 2
3
Điểm: 200

Sample Input 1
4
6
177013
3
555
10
0123456789
6
130505
Sample Output 1
6
3
17
38
Giải thích
- Ở test 1, có ~6~ số thoả mãn điều kiện là: ~0, 10, 70, 170, 770, 1770~;
- Ở test 2, có ~3~ số thoả mãn điều kiện là: ~5, 55, 555~.