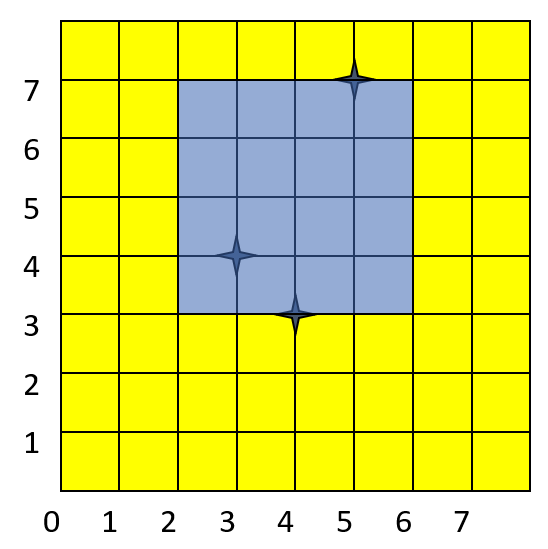
Trên mặt phẳng với hệ tọa độ Descartes vuông góc ~Οxy~ cho ~n~ điểm. Hãy tìm hình vuông nhỏ nhất có cạnh song song với một trong hai trục tọa độ chứa tất cả ~n~ điểm đã cho (điểm nằm trên cạnh hình vuông cũng bị tính là chứa trong hình vuông)

Input:

Vào từ file văn bản "SQUARE.INP":

• Dòng 1 chứa số nguyên dương ~n\le10^5~.
• ~n~ dòng tiếp theo, dòng thứ ~i~ chứa hai số nguyên ~x_i,y_i~ là tọa độ của một điểm ~(x_i,y_i)~, ~\forall i:|x_i|,|y_i|\le10^9~.

Output:

• Ghi ra file văn bản "SQUARE.OUT" một số nguyên duy nhất là diện tích hình vuông tìm được.

Sample Input 1

3
3 4
5 7
4 3

Sample Output 1

16

Giải thích

Cho bốn số nguyên dương ~A,B,C,D~. Hãy đếm xem có bao nhiêu số nguyên dương ~X~ thỏa mãn các điều kiện sau:

1. ~A≤ X ≤ B~
2. ~X~ không chia hết cho ~C~;
3. ~X~ không chia hết cho ~D~;

Dữ liệu: Vào từ file văn bản CNTNUM.INP gồm:

• Một dòng duy nhất ghi bốn số ~A,B,C,D~ ~(1≤A,B≤10^{18}~; ~1≤C,D≤10^9)~.

Kết quả: Ghi ra file văn bản CNTNUM.OUT gồm:

• Một dòng duy nhất ghi số lượng số nguyên dương X thỏa mãn điều kiện của đề bài.

Ví dụ:

Sample Input 1

4 9 2 3

Sample Output 1

2

Cho dãy a gồm n số nguyên dương. Hãy cho biết có bao nhiêu cặp số trong dãy có tổng chia hết cho 3. Nói cách khác, bạn phải đếm xem có bao nhiêu cặp chỉ số ~i,j (1≤i<j≤n)~ sao cho tổng ~a_i+a_j~ chia hết cho 3.</p>

Dữ liệu: Vào từ file văn bản DIV3.INP gồm:

• Dòng 1: Một số nguyên duy nhất ~n (1≤n≤10^5)~.
• Dòng 2: Ghi n số nguyên dương ~a_1,a_2,...,a_n (1≤a_i≤10^5,∀i=1→n)~ là các phần tử của dãy.

Kết quả: Ghi ra file văn bản DIV3.OUT:

• Một dòng duy nhất ghi số lượng cặp số của dãy a có tổng chia hết cho 3.

Ví dụ:

Sample Input 1

5
3 4 2 3 4

Sample Output 1

3

Sample Input 2

4
3 6 9 12

Sample Output 2

6

Cho dãy số nguyên ~A~ gồm ~n~ phần tử ~a_1, a_2, \dots, a_n~. Một dãy chỉ số ~1 \le i_1 < i_2 < \dots < i_k \le n~ mà ~a_{i_1} \le a_{i_2} \le \dots \le a_{i_k}~, khi đó ~a_{i_1} \le a_{i_2} \le \dots \le a_{i_k}~ được gọi là một dãy con tăng của ~A~. Hãy tìm độ dài dãy con tăng không ngặt dài nhất của ~A~.

Input: Vào từ file văn bản LIQ.INP:

• Dòng đầu ghi số nguyên dương ~n~ ~(n \le 1000)~.
• Dòng hai ghi dãy số nguyên ~A~ ~(|A_i| \le 10^9)~.

Output: Ghi ra file văn bản LIQ.OUT:

• Một số nguyên là độ dài dãy con tăng không ngặt dài nhất.

Sample Input 1

6
1 2 5 4 6 2

Sample Output 1

4

Sample Input 2

10
1 2 3 4 9 10 5 6 7 8

Sample Output 2

8

Cho dãy số nguyên ~A~ gồm ~n~ phần tử ~a_1, a_2, \dots, a_n~. Một dãy chỉ số ~1 \le i_1 < i_2 < \dots < i_k \le n~ mà ~a_{i_1} < a_{i_2} < \dots < a_{i_k}~, khi đó ~a_{i_1} < a_{i_2} < \dots < a_{i_k}~ được gọi là một dãy con tăng của ~A~. Hãy tìm độ dài dãy con tăng dài nhất của ~A~.

Input: Vào từ file văn bản LIS.INP:

• Dòng đầu ghi số nguyên dương ~n~ ~(n \le 10^5)~.
• Dòng hai ghi dãy số nguyên ~A~ ~(|A_i| \le 10^9)~.

Output: Ghi ra file văn bản LIS.OUT:

• Dòng 1: Một số nguyên là độ dài dãy con tăng đơn điệu dài nhất.
• Dòng 2: Dãy con tăng dài nhất tìm được, các số ghi cách nhau bởi dấu cách (Nếu có nhiều dãy thì ghi ra dãy có thứ tự từ điển nhỏ nhất)

Sample Input 1

6
1 2 5 4 6 2

Sample Output 1

4
1 2 4 6

Sample Input 2

10
1 2 5 4 6 2 1 2 3 4

Sample Output 2

4
1 2 3 4

Cho dãy gồm ~n~ số nguyên ~a_1,a_2,…,a_n~ ~(1≤a_i≤3,∀i=1→n)~. Có bao nhiêu cách để xóa đi một số phần tử của dãy (không xóa phần tử nào cũng được coi là một cách mà vẫn giữa nguyên thứ tự ban đầu để được một dãy mới thỏa mãn hai yêu cầu sau:

1. Dãy còn ít nhất 3 phần tử;
2. Phần tử đầu tiên của dãy có giá trị 1, tiếp theo là một số phần tử có giá trị là 2 (ít nhất có 1 số 2) và kết thúc bằng đúng một phần tử có giá trị là 3. Ví dụ: các dãy {1, 2, 2, 3} và dãy {1, 2, 3} thỏa mãn yêu cầu; các dãy {1, 2, 3, 3) và dãy {1, 1, 2, 3} không thỏa mãn yêu cầu.

Input: Vào từ file văn bản DELETE.INP:

• Dòng 1: số nguyên dương ~n~ ~(n≤10^6)~ là số lượng phần tử của dãy.
• Dòng 2: ghi ~n~ số nguyên ~a_1,a_2,…,a_n~ là giá trị của các phần tử của dãy ban đầu.

Output: Ghi ra file văn bản DELETE.OUT:

• Gồm một dòng duy nhất là số cách xóa để được dãy mới thỏa mãn yêu cầu của đề bài. Do số lượng cách xóa phần tử có thể rất lớn nên bạn chỉ cần ghi ra số lượng cách xóa sau khi chia lấy dư cho ~(10^9+7)~

Sample Input 1

8
1 2 1 2 3 1 2 3

Sample Output 1

15

Cho dãy ~A~ gồm ~n~ phần tử ~1,2,3,...,n~. Người ta thực hiện trên dãy số này đúng ~k~ lần hai thao tác sau:

1. Đầu tiên, đảo ngược thứ tự (lật đối xứng) đoạn phần tử có chỉ số từ ~u~ đến ~v~.
2. Tiếp theo, đảo ngược thứ tự (lật đối xứng) đoạn phần tử có chỉ số từ ~l~ đến ~r~. Với ~u, v, l, r~ là các hằng số cho trước.

Yêu cầu:

• Hãy đưa dãy ~A~ sau khi thực hiện ~k~ lần 2 thao tác nói trên.

Input: Vào từ file văn bản REVNREV.INP:

• Dòng 1: hai số nguyên dương ~n,k~ ~(1 ≤ n ≤ 100,1≤k≤10^9).~
• Dòng 2: gồm hai số nguyên dương ~u,v~ ~(1≤ u<v≤n).~</li>
• Dòng 3: gồm hai số nguyên dương ~l,r~ ~(1≤l<r≤n).~</li>

Output: Ghi ra file văn bản REVNREV.OUT:

• Ghi trên ~n~ dòng, dòng thứ ~i~ ~(∀i = 1 → n)~ ghi giá trị của phần tử thứ ~i~ của dãy ~A~ sau khi thực hiện ~k~ lần hai thao tác nói trên.

Sample Input 1

7 2
2 5
3 7

Sample Output 1

1
2
4
3
5
7
6