Gần đây, để dễ dàng quản lí, liên bang Berland muốn được chia thành các tiểu bang riêng biệt. Hơn nữa, họ yêu cầu rằng có một tiểu bang bao gồm chính xác ~k~ thị trấn.

Hiện tại, Berland có ~n~ thị trấn, được đánh số từ 1 đến ~n~. Các thị trấn được nối với nhau bằng đường hai chiều. Berland chỉ có ~n-1~ đường. Bạn có thể đến bất kỳ thành phố nào từ thủ đô, nghĩa là mạng lưới đường bộ tạo thành hình cây.

Yêu cầu: Đưa ra kế hoạch chia liên bang thành các tiểu bang nhỏ như sau:

• Trong mỗi tiểu bang, đều có các con đường kết nối các thị trấn trong tiểu bang. Nghĩa là ta có thể đi từ một thị trấn đến một thị trấn bất kì khác trong tiểu bang đó.
• Có ít nhất một tiểu bang bao gồm chính xác ~k~ thị trấn.
• Trong ~n-1~ đường, số lượng đường không được sử dụng là tối thiểu.

Nếu bạn tìm được đúng số lượng đường tối thiểu, bạn được ~30\%~ số điểm của test đó.

Input

Vào từ file BERLAND.INP:

• Dòng đầu chứa số nguyên ~n~, ~k~ ~(1 \le k \le n \le 400)~,
• ~n-1~ dòng tiếp theo, mỗi dòng chứa các cặp số nguyên ~(u, v)\ (1 \le u, v \le n,\ u \neq v)~ mô tả một con đường ở Berland.

Output

Ghi ra tệp BERLAND.OUT:

• Dòng đầu tiên in số đường không được sử dụng tối thiểu ~t~.
• Dòng tiếp theo in ra ~t~ số nguyên là thứ tự nhập của ~t~ con đường đó.
• Nếu có nhiều cách chia, có thể in bất kì cách chia nào.

Sample Input 1

5 3 
1 2 
1 3 
1 4 
1 5

Sample Output 1

2
3 4

Sample Input 2

5 2
1 2
2 3
3 4
4 5

Sample Output 2

1
2

Sample Input 3

1 1

Sample Output 3

0

Giải thích:

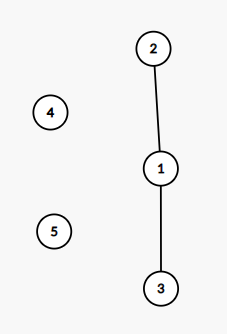
Cách chia của ví dụ đầu tiên nếu ta không sử dụng đường số ~3~ (nối ~1~ và ~4~) và ~4~ (nối ~1~ và ~5~).