Loli rất thích đến thăm bạn Shiina Mahiru - cô gái nhà bên. Vấn đề ở đây là, mặc dù là "nhà bên", nhưng nhà hai đứa lại cách nhau cả một đoạn sông. Loli vì mê gái nên tìm cách xây cả cái cầu để đi cho tiện.

Ta có thể coi đoạn sông là một cái bảng hai chiều gồm ~n~ hàng và ~m~ cột. Giao điểm của hàng thứ ~i~ và cột thứ ~j~ chứa giá trị ~a_{i,j}~ là độ sâu của ô tương ứng. Tất cả các ô ở cột đầu tiên và cột cuối cùng tương ứng với bờ sông, vì vậy độ sâu của chúng là ~0~.

Ví dụ về một đoạn sông:

Loli có thể chọn hàng thứ ~i~, chứa các ô ~(i,1),(i,2),\dots,(i,m)~ và xây cầu trên đó. Trong mỗi ô của hàng đã chọn, Loli có thể lắp đặt một trụ để đỡ cầu. Chi phí lắp đặt trụ đỡ tại ô ~(i,j)~ là ~a_{i,j}+1~.

Trụ đỡ phải được lắp đặt sao cho đáp ứng các điều kiện sau:

• Phải lắp đặt trụ đỡ tại ô ~(i,1)~;
• Phải lắp đặt trụ đỡ tại ô ~(i,m)~;
• Khoảng cách giữa bất kỳ cặp trụ đỡ liền kề nào không được vượt quá ~d~, trong đó khoảng cách giữa trụ đỡ ~(i,j_1)~ và ~(i,j_2)~ là ~|j_1-j_2|-1~.

Chỉ xây một cây cầu thì hơi dễ. Do đó, để sĩ với Mahiru, Loli sẽ xây cầu trên các hàng sông liên tiếp, tức là chọn ~i\ (1\le i \le n-k+1)~ và độc lập xây dựng cầu trên mỗi hàng ~i,i+1,\dots,i+k-1~.

Lưu ý rằng các cây cầu trên các hàng không nhất thiết phải có các trụ đỡ thẳng cột với nhau (nói cách khác, mỗi cây cầu đều được xây dựng riêng lẻ, không liên quan đến cây cầu khác).

Bạn hãy giúp Loli flex ví tiền của mình bằng cách tìm cách xây cầu tiết kiệm nhất.

Input

• Dòng đầu tiên chứa bốn số nguyên dương ~n,m,k,d~ ~(1\le k\le n\le 50,\ 3\le m\le 2\times 10^5,\ 1\le d\le m)~, lần lượt là số hàng và số cột, số cây cầu xây liên tiếp và khoảng cách tối đa giữa các trụ đỡ.
• Tiếp theo là ~n~ dòng, dòng thứ ~i~ chứa ~m~ số nguyên dương ~a_{i,j}~ ~(0\le a_{i,j}\le 10^6,\ a_{i,1}=a_{i,m}=0)~ là độ sâu của các ô sông.
• Test đảm bảo tích ~n\times m~ không vượt quá ~2\times 10^5~.

Output

• Hãy in ra một số duy nhất là tổng chi phí tối thiểu để lắp đặt trụ đỡ.

Subtasks

• Subtask 1: ~30\%~ test có ~m \le 10~;
• Subtask 2: ~30\%~ test có ~m \le 1000~;
• Subtask 3: ~40\%~ test còn lại không có ràng buộc gì thêm.

Sample Input 1

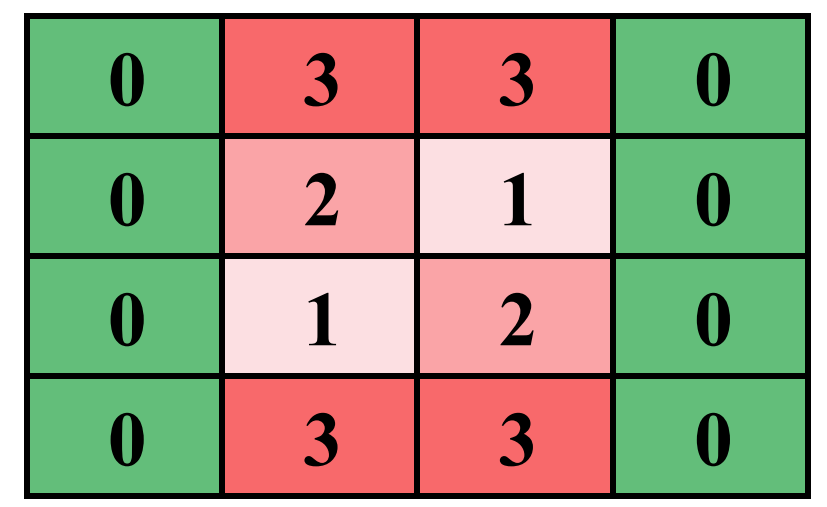
4 4 2 1
0 3 3 0
0 2 1 0
0 1 2 0
0 3 3 0

Sample Output 1

8

Giải thích:

Ở test đầu tiên:

• Để xây cầu ở hàng 1, đặt trụ ở cột ~1, 2, 4~ là tiết kiệm nhất. Chi phí là ~1 + 4 + 1 = 6~.
• Để xây cầu ở hàng 2, đặt trụ ở cột ~1, 3, 4~ là tiết kiệm nhất. Chi phí là ~1 + 2 + 1 = 4~.
• Để xây cầu ở hàng 3, đặt trụ ở cột ~1, 2, 4~ là tiết kiệm nhất. Chi phí là ~1 + 2 + 1 = 4~.
• Để xây cầu ở hàng 4, đặt trụ ở cột ~1, 2, 4~ là tiết kiệm nhất. Chi phí là ~1 + 4 + 1 = 6~.

Ta cần phải xây liên tiếp 2 cây cầu, vậy ta sẽ chọn xây ở hàng 2 và 3 sẽ là tiết kiệm nhất. Tổng chi phí là ~4+4 = 8~.