Chính phủ quốc đảo Oceani quyết định xây dựng ~m~ chiếc cầu nối ~n~ đảo của mình, tạo một mạng lưới giao thông đường bộ cho phép đi từ dảo bất kỳ tới đảo khác bằng đường bộ (trực tiếp hoặc qua một số đảo trung gian). Mỗi cây cầu sẽ nối ~2~ đảo khác nhau và cho phép đi lại hai chiều. Các đảo được đánh số từ ~0~ đến ~n-1~. Bị hạn chế bởi kinh phí và nguồn nhân lực, người ta quyết định sẽ xây dựng lần lượt từng chiếc cầu một và lên kế hoạch xác định cầu và trình tự xây. Mỗi cây cầu được xác định bởi cặp đảo ~u~, ~v~ mà nó nối. Trong quá trình thực hiện kế hoạch có thể đến một lúc nào đó từ một đảo đã có thể đi đến bất kỳ đảo khác bằng đường bộ.

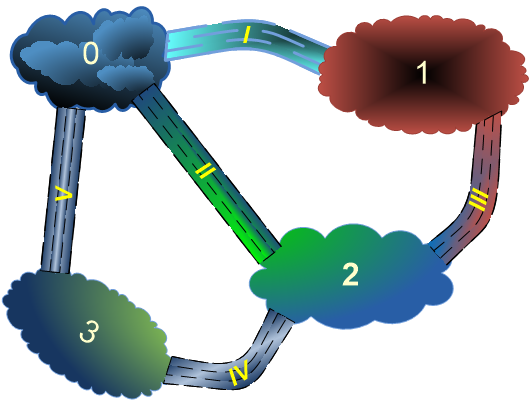
Ví dụ, ở Oceani có ~4~ đảo và người ta quyết định xây dựng ~5~ cầu theo trình tự lần lượt là ~0 – 1, 0 – 2, 1 – 2, 2 – 3, 3 – 0~. Tuy vậy, không cần chờ đợi đến khi hoàn thành kế hoạch xây cầu, sau khi cầu thứ ~4~ được xây xong tất cả các đảo đã được nối liền bằng đường bộ.

Yêu cầu: Cho ~n~, ~m~ và các cây cầu dự kiến xây. Thông tin về các cây cầu đưa ra theo đúng trình tự xây dựng. Hãy xác định số cầu tối thiểu cần xây theo kế hoạch để từ một đảo đã có thể đi đến bất kỳ đảo khác bằng đường bộ.

Input

• Dòng đầu tiên chứa ~2~ số nguyên ~n~ và ~m~ ~(1 \le n \le 10^6,\ 1 \le m \le 5*10^6)~,
• Dòng thứ ~i~ trong ~m~ dòng tiếp theo chứa ~2~ số nguyên ~u~ và ~v~ xác định cây cầu thứ ~i~ cần xây.

Output

• Một số nguyên – kết quả tìm được.

Sample Input

4 5
0 1
0 2
1 2
2 3
3 0

Sample Output

4