Loli tự hào khi có bộ sưu tập xuân hạ thu đông, gồm có ~n~ bức ảnh chụp ảnh các chị gái xinh đẹp trong anime, quả mướp ăn nướng. Mỗi bức ảnh có kích cỡ khác nhau, nhưng chúng đều là hình vuông, bức ảnh thứ ~i~ có chiều dài cạnh là ~s_i\ (cm)~.

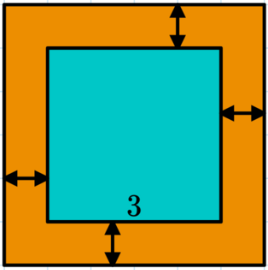
Chẳng lẽ một bộ sưu tập đồ sộ như này lại bị chôn vùi dưới ngăn bàn suốt trăm năm? Nô nô, Loli định treo chúng lên. Mỗi bức ảnh được treo lên sẽ cần một cái khung. Bức ảnh sẽ được đặt ở chính giữa, và khung sẽ có độ rộng viền là ~w~. Mọi bức ảnh đều có viền có độ rộng giống nhau. Ví dụ: Loli có một bức ảnh ~3\times 3~, và Loli muốn viền các bức ảnh rộng ~1\ (cm)~. Vậy khung ảnh cuối cùng sẽ có kích cỡ là ~5\times 5~, và Loli cần ~25\ cm^2~ bìa để làm khung tranh đó.

Trong nhà Loli hiện có tổng ~c\ (cm^2)~ bìa (để dùng làm khung ảnh), và bằng một cách thần kỳ nào đó, chúng đã được cắt rất hợp lý để mỗi bức ảnh đều có một cái khung tương ứng, chắc là Loli đã cắt từ trước nhưng mải chơi nên quên mất. Thậm chí Loli còn quên cả độ rộng ~w~ của viền ảnh??

Yêu cầu: Tìm lại độ rộng viền ~w~ của các khung ảnh, sao cho tổng diện tích bìa của các khung ảnh bằng ~c~.

Input

• Dòng thứ nhất chứa một số nguyên ~t\ (1\le t \le 1000)~ là số test con.
• Mỗi test con đều có:
  • Dòng đầu chứa 2 số nguyên dương ~n\ (1\le n\le 2\times 10^5)~ và ~c\ (1\le c\le 10^{18})~ là số ảnh và tổng diện tích bìa.
  • Dòng thứ hai chứa ~n~ số nguyên dương ~s_i\ (1\le s_i\le 10^4)~ là chiều dài cạnh của ảnh ~i~.
• Test đảm bảo tổng số lượng ~n~ không vượt quá ~2\times 10^5~.

Output

• Gồm ~t~ dòng, dòng ~i~ chứa một số nguyên duy nhất là kết quả của test con thứ ~i~.

Subtasks

• Testcase 1: ~15\%~ số test có ~n\le 100~ và ~c\le 10^4~.
• Testcase 2: ~15\%~ số test có ~n\le 100~.
• Testcase 3: ~15\%~ số test có ~c\le 10^4~.
• Testcase 4: ~15\%~ số test có ~c\le 10^9~.
• Testcase 5: ~40\%~ số test không có ràng buộc gì thêm.

Sample Input 1

2
3 50
3 2 1
5 500
2 2 2 2 2

Sample Output 1

1
4

Giải thích:

Ở test đầu, với đáp số ~w = 1~, ta có tổng diện tích bìa là ~c = (3 + 1\times 2)^2 + (2 + 1\times 2)^2 + (1 + 1\times 2)^2 = 50~.

Ở test thứ 2, với đáp số ~w = 4~, ta có tổng diện tích bìa là ~c = (2 + 4\times 2)^2 \times 5 = 100 \times 5 = 500~.